REFLECTIVITY-RAINFALL RATE RELATIONSHIPS IN OPERATIONAL METEOROLOGY
Jeffrey D. Fournier
April 1999
ABSTRACT
The National Weather Service has a very low ratio of rain gages per area. This makes it very difficult to accurately assess rainfall amounts based on gage data alone. As early as 1947, a paper published by Marshall et al. attempted to address this problem by correlating radar reflectivity values (Z) with rainfall rates (R). Today, the National Weather Service uses Z = 300 R^1.4 as the primary default Z-R relationship for the WSR-88D radar network.
There are certain situations where this relationship does not hold. One example was tropical storm Josephine in October, 1996. The default Z-R relationship was used during this event, causing the WSR-88D in Tallahassee, Florida to severely underestimate rainfall totals across north Florida and south Georgia. However, when a special tropical Z-R relationship was used for the same data, the result was an overestimation of rainfall across the same area. Since Josephine exhibited many subtropical characteristics, intuition suggests fitting a new Z-R curve in between the default and tropical Z-R curves; but there are several arguments against such an approach.
1. Introduction
In southeast Alabama, southwest Georgia, and northwest Florida, there is about one regularly-reporting National Weather Service rain gage for every 7,700 square kilometers. River Forecast Center computer models used to forecast river stages rely heavily on accurate rainfall amounts. In scattered convective situations, heavy rainfall can occur across portions of a river basin, and still miss several of the rain gages. This can lead to erroneous stage forecasts. Also, if a gage breaks, or appears to be giving faulty readings, it would be useful to have another source for comparison of rainfall amounts.
Fortunately, these problem have been nearly solved by advances in radar. Shortly after the development of weather radar, Marshall et al. (1947) reported a good correlation between reflectivity (Z) and rainfall rate (R). Z is dependant on the raindrop size distribution and the size of the drops (to the sixth power). R is dependant on the raindrop size distribution, the size of the drops (to the third power), and the fall velocity for a given drop diameter. Because of these different relationships, the Z-R relationship is not unique; as there can be different rainfall rates for a particular reflectivity, and vice-versa.
Marshall-Palmer (1948) contained the results of research relating size distribution of raindrops as a function of rainfall rate. From this relationship, the famous Marshall and Palmer relationship of Z = 200 R^1.6 was derived (where 200 and 1.6 are empirical constants (Rinehart,1991)). Although several other empirical constants have been determined, the National Weather Service used the Marshall and Palmer Z-R relationship for its network of WSR-57 weather radars. When the National Weather Service replaced the WSR-57 radars with the more sophisticated WSR-88D radars, the Z-R relationship was changed to Z = 300 R^1.4. This was done to minimize both the overestimation of light precipitation and underestimation of heavy precipitation. Studies by the National Weather Service (using extensive conventional weather radar data from previous Z-R relationships) have shown this newer relationship to be valid over most of the eastern two-thirds of the country (OSF Staff).
While the newer WSR-88D default Z-R relationship works well in most operational settings, there are some significant limitations. Hail contamination can cause overestimation of rainfall rates. To compensate for this, the WSR-88D employs an algorithm that truncates any rainfall rate greater than 103.9 mm/hour. Research has also shown that during tropical convection, the current default Z-R relationship underestimates rainfall rates. During tropical situations, the National Weather Service allows individual offices to change the default relationship to Z = 250 R^1.2; which has been shown to estimate rainfall rates more accurately in these situations.
In October, 1996, tropical storm Josephine moved across much of north Florida and south Georgia, causing very heavy rains. This paper will compare how much rainfall occurred based on rain gage data, the WSR-88D default Z-R relationship, and the tropical Z-R relationship. Also, the possibilities of a better Z-R relationship will be explored.
2. Methods
a. Brief summary of equations used
Z = Integral [N(D) D^6 dD] R = (PI / 6) * Integral [N(D) D^3 W(D) dD]
where:
Z=reflectivity factor
R=rainfall rate
D=raindrop diameter
N(D)=number of drops of given diameter per cubic meter
W=fall velocity for a given diameter
This is the theoretical definition of reflectivity (Z). However, the WSR-88D is not able to observe raindrop size distribution or raindrop size, so Z must be determined from the simplified radar equation:
Z = (Power Returned * Target range^2) / radar constant
This equations assumes Rayleigh scattering, which occurs with targets whose diameter is much smaller than the wavelength of the transmitted electromagnetic radiation (Battan, 1973). The WSR-88D uses a wavelength of approximately 10.7 cm, and almost all raindrops have diameters of 7 mm or less.
Extensive research has shown that, in general, Z = A * R^b, where A and b are empirically determined constants.
b. Brief synopsis of Josephine rainfall event
Tropical storm Josephine moved across Apalachee Bay, north Florida, and south Georgia on the 7th and 8th of October, 1996. By the time the center moved inland, the storm was already losing its tropical characteristics. This was indicated by the asymmetric cloud structure, and especially by surface data. In fact, the surface temperature at Keaton Beach (near the point of landfall) fell about 6 degrees C in one hour shortly after landfall (Pasch, 1997). Rapid and significant temperature changes like this do not occur in purely tropical systems. Josephine would have been better described as subtropical near the time of landfall, as the system exhibited tropical and extra-tropical characteristics.
c. Rainfall data collection
During this period, relatively steady, heavy rainfall occurred across north Florida and south Georgia. The WSR-88D was calculating rainfall amounts using the default Z-R relationship of
Z = 300 R^1.4. After the event, rainfall totals were recalculated using the tropical Z-R relationship of Z = 250 R^1.2. This was done by using archive level II data, which is basically a continuous, high-resolution recording of raw data collected at the Radar Data Acquisition (RDA). The data was then used in WSR-88D Algorithm Testing and Display System (WATADS), where the tropical Z-R was applied. Also, 24-hour rainfall totals were collected from the National Weather Service rain gage network across north Florida and south Georgia. The three sets of data were plotted, using color contours on GEMPAK, and stored for future use.
3. Results
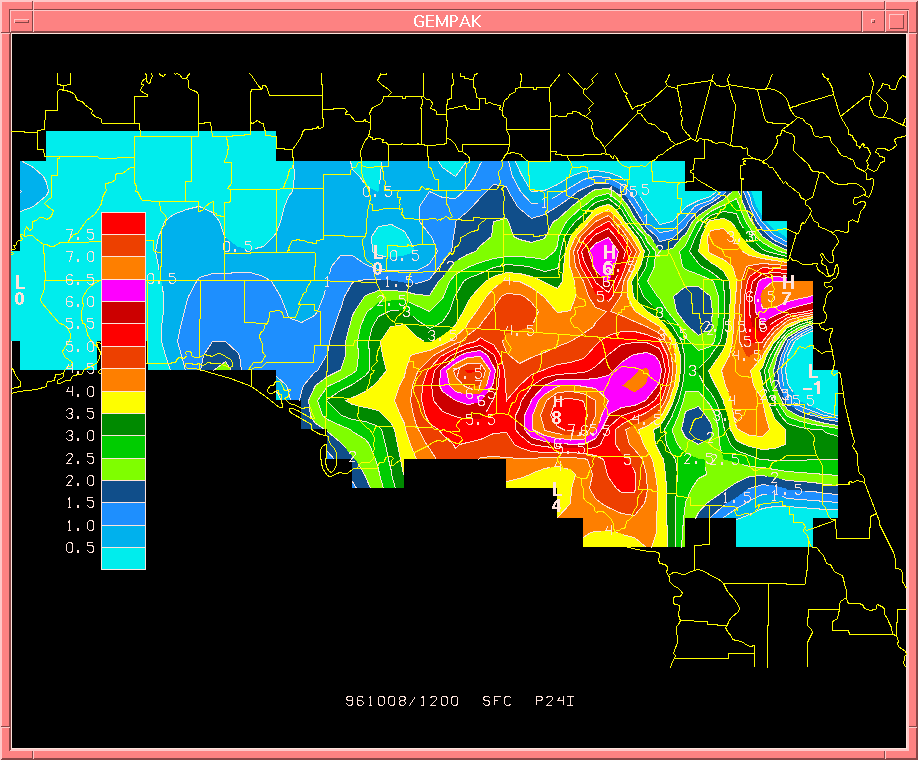
FIG. 1. Actual 24-hour rainfall totals (in inches) for October 7-8, ending at 12 UTC, based on rain gage data across north Florida and south Georgia.
Although interpolated values suffer somewhat due to the sparse gage network, the overall pattern is in reasonably good agreement with the radar estimations (seen on the next page).
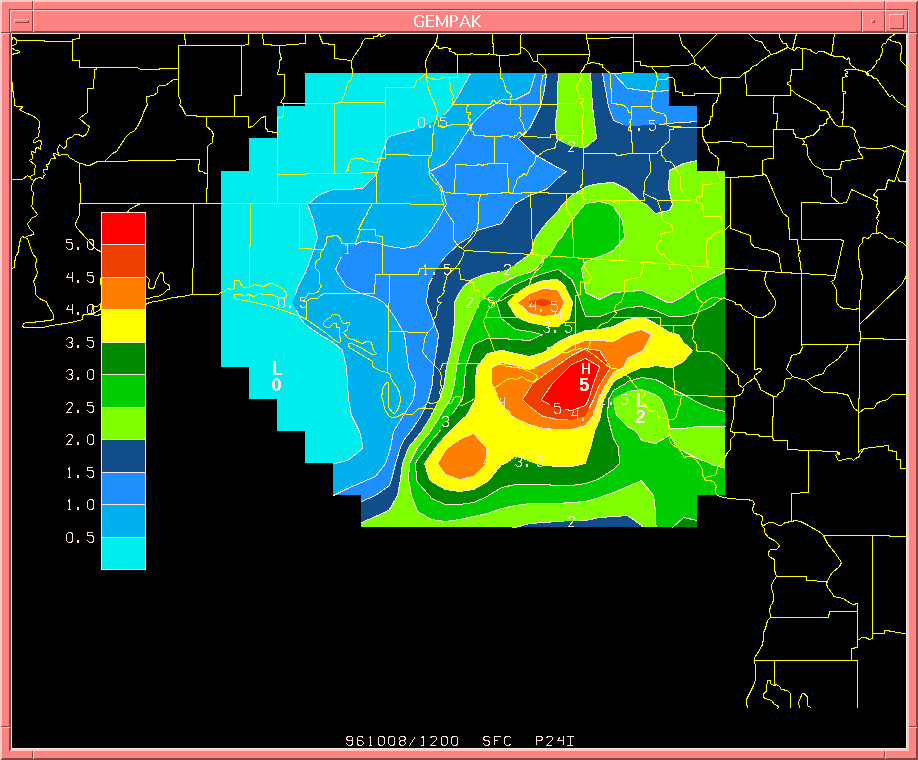
FIG. 2. 24-hour rainfall totals (in inches) during the same period, using the WSR-88D default Z-R relationship of
Z = 300 R^1.4.
Note the maximum values over Taylor and Leon Counties (Florida) are less than that measured by the gage network.
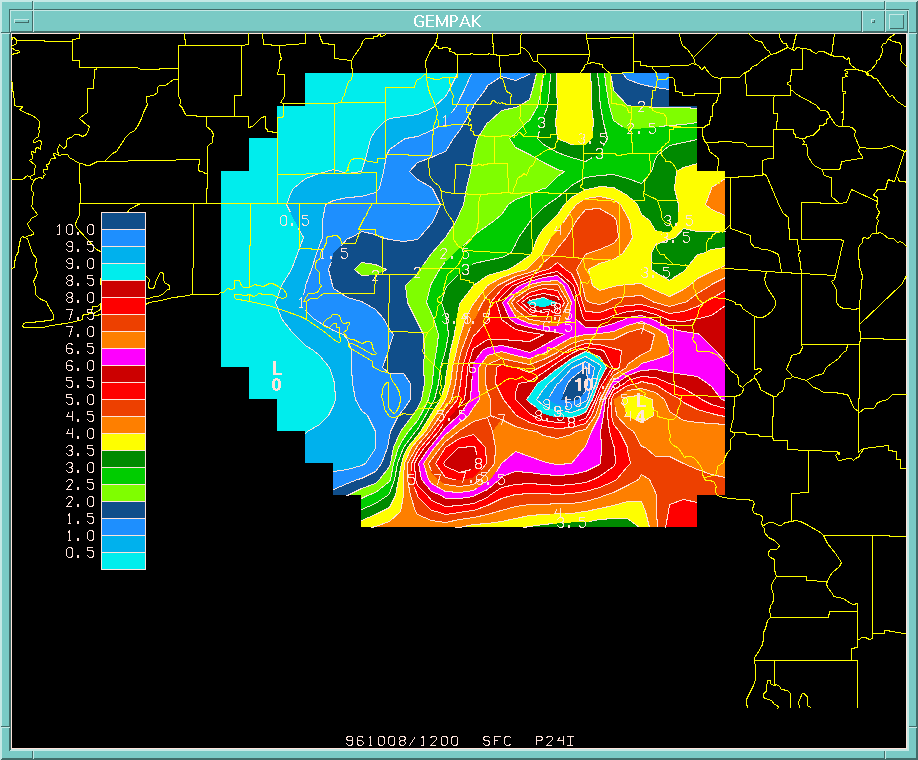
FIG. 3. 24-hour rainfall totals (in inches) during the same period, using the WSR-88D tropical Z-R relationship of
Z = 250 R^1.2.
Here the maximum value over Taylor county agrees quite well with the actual gage data. However, the Leon county maximum shown here is much greater than that measured by the gage network.
4. Conclusions
While research has shown that the current WSR-88D default Z-R relationship performs better than the old Marshall and Palmer Z-R relationship, it still has some deficiencies, especially in dealing with tropical situations. However, the tropical Z-R relationship (which traditionally performs better than the default Z-R relationship in tropical situations), overestimated rainfall totals in this particular case. The fact that Josephine was subtropical may explain why actual gage-reported values fell in between the two different radar estimates. Does this warrant determining yet another Z-R relationship?
Smith et al. (1990) says, "there is no substantive reason to believe that efforts to determine space or time-dependent Z-R relationships will lead to improvements commensurate with the effort required". This statement was based on previous research from the 1970s, where several studies showed virtually no improvement at rainfall estimation among the wide variety of empirically determined Z-R relationships. In fact, Lovejoy and Austin (1979) argued that reasonably accurate rainfall estimates could be obtained by using radar to estimate the total area of rainfall, and then multiplying by a climatological rainfall rate. Indeed, Battan (1973) lists more than 60 experimentally determined Z-R relationships, and many more have been produced since that paper (Rinehart, 1991).
An operational meteorologist working in the field may not have time to sort through a lengthy list for the ideal Z-R relationship to fit a particular synoptic situation. This, coupled with the arguments presented above, are at odds with the notion of simply trying to find a Z-R curve that lies between the default and tropical Z-R relationships for a subtropical storm. Unless there is a major breakthrough in Z-R relationship research, the best operational approach may be a qualitative one. The radar operator (and the hydrologist running a river forecast model) will have to recognize the inherent deficiencies of each Z-R relationship, and qualitatively adjust accordingly in a subtropical situation.
Acknowledgments. The author wishes to thank A. I. Watson for compiling, analyzing, and saving all of the Josephine rainfall data used in this paper.
References
Doviak, R. J. and Zrnic', D. S., 1984: Doppler Radar and Weather Observations. Academic Press, Inc. 458 pages.
Atlas, D. (editor), 1990: RADAR in Meteorology. American Meteorological Society, Boston, Massachusetts. 806 pages.
Rinehart, R.E., 1991: RADAR for Meteorologists. Ronald E. Rinehart, Grand Forks, North Dakota. 334 pages.
Staff, circa 1990: Principles of Meteorological Doppler Radar. OSF, Operations Training Branch, Norman, Oklahoma. 47 pages.
Pasch, R. J., 1997: Preliminary Report: Tropical Storm Josephine 4-8 October 1996. National Hurricane Center, http://www.nhc.noaa.gov/data/tcr/AL101996_Josephine.pdf​